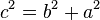ecuaciones:
Una
ecuación es una igualdad entre dos
expresiones algebraicas, denominadas
miembros, en las que aparecen valores conocidos o
datos, y desconocidos o
incógnitas, relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser
números,
coeficientes o
constantes; y también
variables cuya magnitud se haya establecido como resultado de otras operaciones. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar. Por ejemplo, en la ecuación:

abaco:
Un
ábaco es un objeto que sirve para facilitar cálculos sencillos (sumas, restas y multiplicaciones) y operaciones aritméticas. También es un cuadro de madera con alambres paralelos por los que corren bolas movibles y que sirve para enseñar el cálculo. Su origen se remonta a la zona de Asia Menor, muchos años antes de nuestra era
yupana(matematica incaica):
En el campo de la
matemática los
incaicos destacaron principalmente por su capacidad de cálculo en el ámbito económico. Los
quipus y
yupanas fueron señal de la importancia que tuvo la matemática en la administración incaica. Esto dotó a los incas de una
aritmética sencilla pero efectiva, para fines contables, basada en el
sistema decimal; desconocieron el
cero, pero dominaron la suma, la resta, la multiplicación y la división.
funciones:
En
matemáticas, una
función,
[1] aplicación o
mapeo f es una
relación entre un conjunto dado
X (el
dominio) y otro conjunto de elementos
Y (el
codominio) de forma que a cada elemento
x del dominio le
corresponde un único elemento del codominio
f(x). Se denota por:

productos notables:
Productos notables es el nombre que reciben aquellas
multiplicaciones con
expresiones algebraicas cuyo resultado puede ser escrito por simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales
 imagen del promedio
imagen del promedio
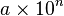
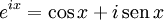
 y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que: